シュレディンガー方程式を導入した際に定義したハミルトニアン演算子は、波動関数から固有値としてエネルギーを取り出すものでした。
ここでは、もう少し広く演算子と言う概念の性質に触れてみたいと思います。
交換関係
演算子の構造は微分などが含まれており、異なる構造を持つ複数の演算子を関数に作用させた場合、演算子を作用させた順番により関数から取り出す情報が異なる場合が多々ある。
そこで今回は演算子Aと演算子Bを例として、演算結果についていくつか定義しておく。まず、2つの演算子の入れ替えの差を[ ]を用いて、
$$\left[\hat{A},\ \hat{B}\right]=\hat{A}\hat{B}-\hat{B}\hat{A}\qquad(1)$$
と定義する。これを交換関係と言う。
可換と非可換
波動関数 を交換関係の右側から作用させた場合、
$$\left[\hat{A},\ \hat{B}\right]\Psi=0\qquad(2)$$
となり、演算子の入れ替えに対して、差が無い場合を演算子の置き換えが可能と言う意味で可換と言う。
また、交換関係において、
$$\left[\hat{A},\ \hat{B}\right]\Psi=i\hat{C}\Psi\qquad(3)$$
の様に、値の差Cが出る場合は、演算子の置き換えにより値が異なる事を意味する。この様な場合を非可換と言う。
位置と運動量の交換関係
例として位置と運動量の交換関係を求める。まず、位置と運動量の交換関係に、波動関数を右から作用させると、
$$\begin{eqnarray*}\left[\hat{x},\ \hat{p}\right]\Psi&=&\left(\hat{x}\hat{p}-\hat{p}\hat{x}\right)\Psi=x(-iħ\frac{∂}{∂x}Ψ)-(-iħ\frac{∂}{∂x})xΨ\\&=&-iħx(\frac{∂Ψ}{∂x})+iħ\frac{∂}{∂x}xΨ=-iħx(\frac{∂Ψ}{∂x})+iħ(Ψ+x\frac{∂Ψ}{∂x})\\&=&iħΨ\qquad(4)\end{eqnarray*}$$
となる。よって、位置と運動量は非可換であり、(4)の結果から交換関係は、
$$\left[\hat{x},\ \hat{p}\right]=iħ\qquad(5)$$
となる。
まとめ
交換関係の基本的な性質を確認することができた。
#演算子 #交換関係 #位置 #運動量 #可換 #非可換 #量子力学 #たくぶつり
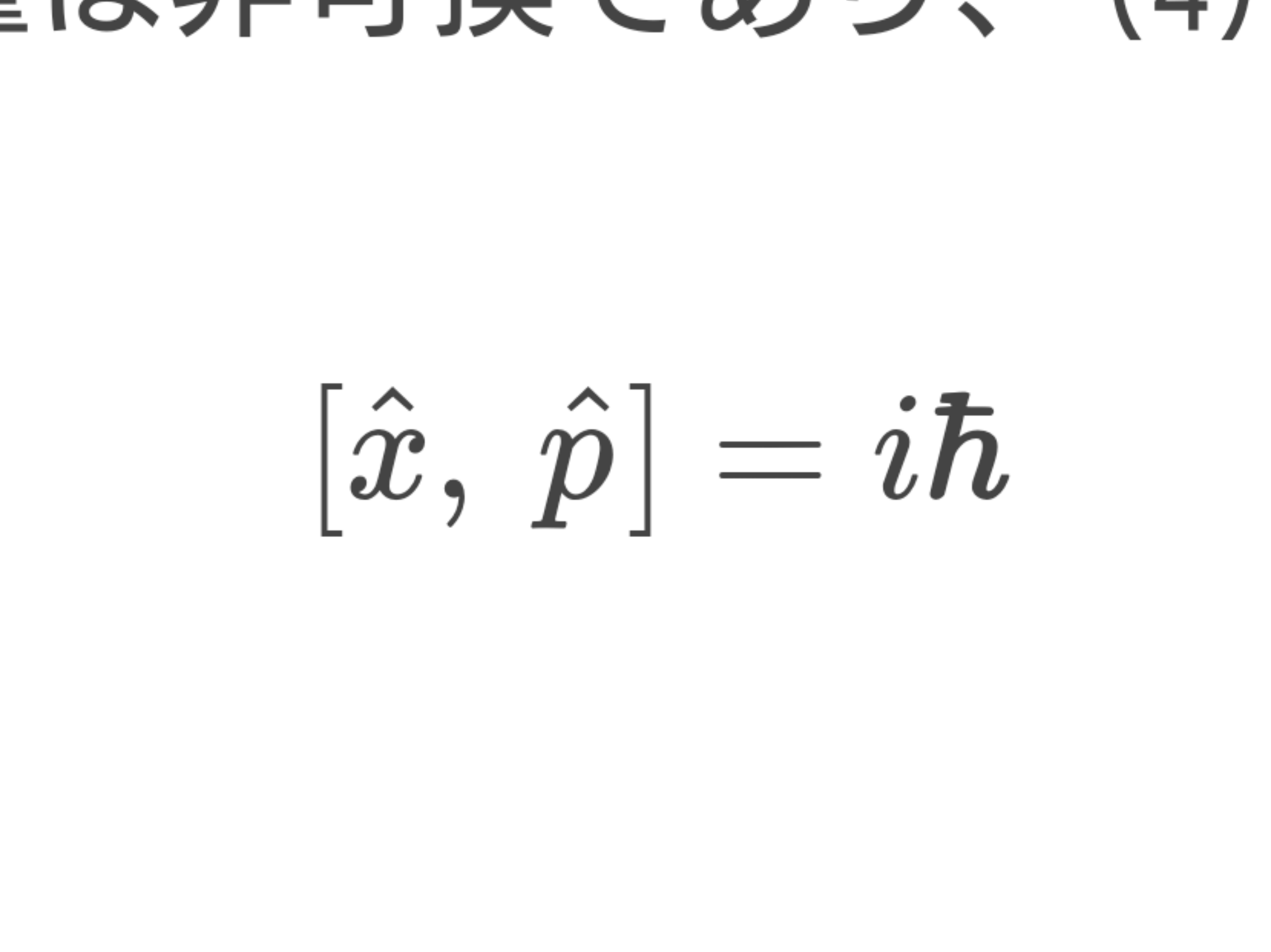


コメント