第８章　波動関数の反射と透過

　電子をポテンシャルで閉じ込められない状態を考える。その際、ポテンシャルの壁では波の反射と透過が起こる。また、電子がポテンシャルの壁を透過する現象をトンネル効果と言う。

確率密度の保存
階段ポテンシャル
トンネル効果

確率密度の保存

　電磁気学のおける電荷密度の保存則と同様に、確率密度についても保存則が成り立つ。まず、確率密度を時間で微分すると

$$\begin{align}\frac{\partial}{\partial\ t}\left|\Psi\left(x,t\right)\right|^2&=\frac{\partial}{\partial\ t}\left(\Psi^\ast\left(x,t\right)\Psi\left(x,t\right)\right)\\&=\frac{\partial\Psi^\ast\left(x,t\right)}{\partial\ t}\Psi\left(x,t\right)-\Psi^\ast\left(x,t\right)\frac{\partial\Psi\left(x,t\right)}{\partial\ t}\qquad(1)\end{align}$$

となる。ここで、シュレディンガー方程式とその共役

$$\frac{\partial\Psi\left(x,t\right)}{\partial\ t}=\frac{iħ}{2m}\frac{∂^2Ψ(x,t)}{∂x^2}+\frac{V(x)}{iħ}Ψ(x,t)\qquad(2)$$

$$\frac{\partial\Psi^\ast\left(x,t\right)}{\partial\ t}=-\frac{iħ}{2m}\frac{∂^2Ψ^\ast(x,t)}{∂x^2}-\frac{V^\ast(x)}{iħ}Ψ^\ast(x,t)\qquad(3)$$

を用いて時間微分を位置の微分に書き換えると

$$\begin{align}\frac{\partial}{\partial\ t}\left|\Psi\left(x,t\right)\right|^2&=-\frac{iħ}{2m}(\frac{∂^2Ψ^*(x,t)}{∂x^2}Ψ(x,t)-Ψ^*(x,t)\frac{∂^2Ψ(x,t)}{∂x^2})\\&=\frac{ħ}{2mi}\frac{∂}{∂x}(\frac{∂Ψ^*(x,t)}{∂x}Ψ(x,t)-Ψ^*(x,t)\frac{∂Ψ(x,t)}{∂x})\qquad(4)\end{align}$$

となる。ここで、確率密度を

$$j\left(x,\ t\right)=\frac{ħ}{2mi}(Ψ^*(x,t)\frac{∂Ψ(x,t)}{∂x}-\frac{∂Ψ^*(x,t)}{∂x}Ψ(x,t))\qquad(5)$$

と定義すると(3.04)式は

$$\frac{\partial}{\partial\ t}\left|\Psi\left(x,t\right)\right|^2=-\frac{\partial}{\partial\ x}j\left(x,\ t\right)\qquad(6)$$

となり、確率密度の保存則が導かれた。

階段ポテンシャル

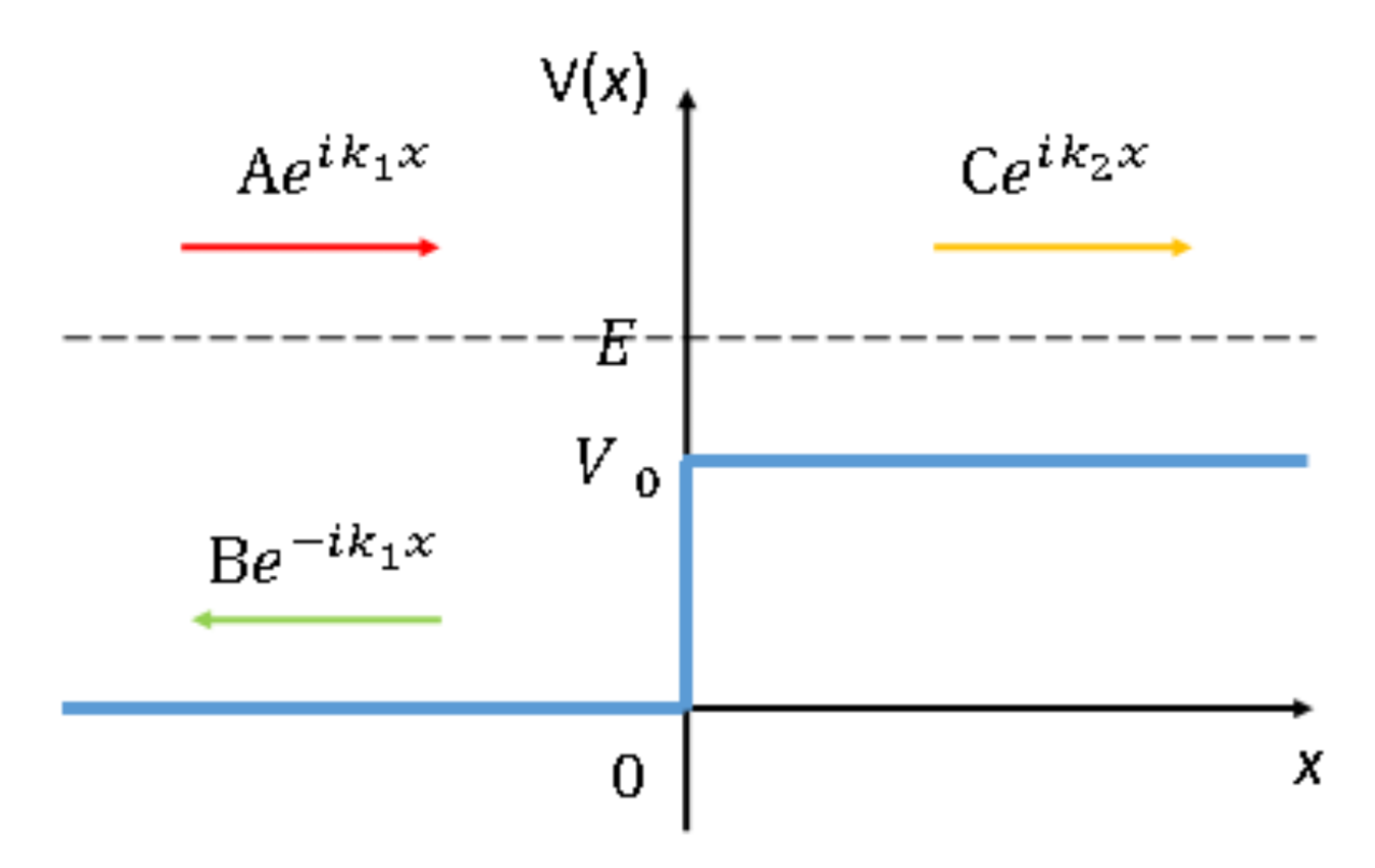
まず、x<0においてV(x)=0、0<xにおいてV(x)=V₀の値を取る図１の様な階段ポテンシャルについて考える。

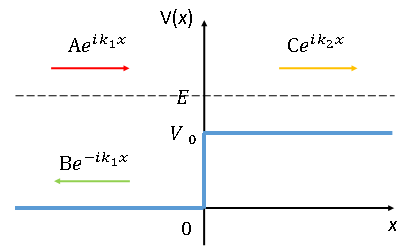
このとき、波動関数は

　ⅰ)　x<0のとき

$$\emptyset_1\left(x\right)=Ae^{ik_1x}+Be^{-ik_1x}\qquad(7)$$

　ⅱ)　\ 0<xのとき

$$\emptyset_2\left(x\right)=Ce^{ik_2x}\qquad(8)$$

となる。ここで、波の進行する方向性から(7)の第１項を入射波、第２項を反射波、(8)を透過波と言う。また、入射波の係数を基準としてA=1、反射波の係数をB=R、透過波の係数をC=Tとする。次に、x<0における確率密度の流れを計算すると

$$j_1\left(x\right)=\frac{ħk_1}{m}(1-|R|^2)\qquad(9)$$

となり、0<xにおける確率密度の流れを計算すると

$$j_2\left(x\right)=\frac{ħk_2}{m}|T|^2\qquad(10)$$

となる。このとき、確率密度の流れは保存するので、j₁(x)=j₂(x)となり、

$$\frac{k_1}{k_2}\left|T\right|^2+\left|R\right|^2=1\qquad(11)$$

となる。また、x<0 と 0<x において、ポテンシャルV(x)の大きさが同じ場合には、k₁=k₂となるので、

$$\left|T\right|^2+\left|R\right|^2=1\qquad(12)$$

となる。

トンネル効果

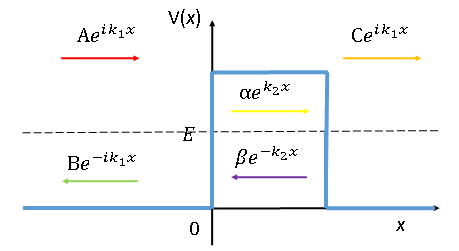
古典力学の考えでは運動エネルギーの保存則により、それを超えるポテンシャルの運動は行うことができない。しかしながら、量子論の場合は確率論の考え方から、図３－２の様に電子がポテンシャルの壁を透過する可能性がある。これにより、十分にポテンシャルの障壁を越えるエネルギーが無くても突破してしまう現象は、ポテンシャルの障壁にトンネルを掘って電子が進むと比喩して、トンネル効果と呼ばれる。