量子力学で最も有名と思われる方程式、シュレディンガー方程式の導出方法について話です。
波動関数
前回の議論で、電子は物質と波の性質も持つと言う話をした。そこで、電子を波束と言う波と解釈し、その性質を示す波導関数を導入する。
まずは、古典力学的なパラメーターを用いると、電子の波動関数は、
$$\Psi\left(x,t\right)=Ae^{i\left(kx-\omega\ t\right)}\qquad(1)$$
となる。このとき、Aを任意の定数、kを波数、xを位置、ωを角振動数、tを時間とした。
この波動関数はx軸上のある時刻tにおける電子の物質波の様子を表現していることになる。また、複素数を導入した理由としては、波の進行方向に区別をつけるためである。詳しく知りたい方は、位相を調べて貰うと良いだろう。
次に、この波動関数のパラメーターを、物質性から波動性を示すパラメーターに書き換える。ここで、区間2π毎に波長λの波が波数k個あると考えると、
$$2\pi=\lambda k\qquad(2)$$
となる。運動量をプランク定数で表現すると、
$$p=\frac{h}{\lambda}\qquad(3)$$
となる。よって、(2)に(3)を代入して整理すると、波数kは、
$$k=\frac{p}{ħ}\qquad(4)$$
となる。このとき、ħ=h/2πとした。
また、角振動数と振動数の関係は、
$$\omega=2\pi\nu\qquad(5)$$
となる。エネルギーと振動数の関係は、
$$E=hν\qquad(6)$$
となる。よって、(5)に(6)を代入すると、
$$\omega=\frac{E}{ħ}\qquad(7)$$
となる。ゆえに、(1)に(3)と(7)を代入すると、
$$\Psi\left(x,t\right)=Ae^{i(px-Et)/ħ}\qquad(8)$$
となる。よって、波動関数において、振動から観測できる波数や角振動数のパラメーターを、光子の様なエネルギーと運動量のパラメーターを用いて表現することができた。
シュレディンガー方程式
波束の状態を示す波動関数のみ分かっていてもあまり意味がない。そこで、波動関数が従う方程式が必要となる。
まず、全エネルギーについて考えと、全エネルギーEは運動エネルギーTとポテンシャルエネルギーUを用いて、
$$\begin{eqnarray*}E&=&T+U\\&=&\frac{1}{2}mv^2+U\qquad(9)\end{eqnarray*}$$
となることが知られている。ここで、運動量p=mvを(9)に代入すると、
$$E=\frac{p^2}{2m}+U\qquad(10)$$
となる。
次に、expの形式の波動関数を微分することにより、pとEの情報を波動関数から取り出すことを考える。まず、(8)をxについて微分すると、
$$\frac{\partial\Psi\left(x,t\right)}{\partial\ x}=i\frac{p}{ħ}Ψ(x,t)\qquad(11)$$
となる。よって、pの変換式は、
$$p\rightarrow-iħ\frac{∂}{∂x}\qquad(12)$$
となる。また、2階微分の場合は、
$$\frac{\partial^2\Psi\left(x,t\right)}{\partial\ x^2}=-\frac{p^2}{ħ^2}Ψ(x,t)\qquad(13)$$
となる。よって、p^2の変換式は、
$$p^2\rightarrow-ħ^2\frac{∂^2}{∂x^2}\qquad(14)$$
となる。
同様に、tについて微分すると、
$$\frac{\partial\Psi\left(x,t\right)}{\partial\ t}=-i\frac{E}{ħ}Ψ(x,t)\qquad(15)$$
となる。よって、Eの変換式は、
$$E\rightarrow iħ\frac{∂}{∂t}\qquad(16)$$
となる。
以上より、(10)に(14)と(16)を代入すると、
$$iħ\frac{∂}{∂t}=-\frac{ħ^2}{2m}\frac{∂^2}{∂x^2}+U\qquad(17)$$
となる。ここで、Uに位置xに依存するポテンシャルV(x)を導入し、右側から波動関数を掛けると、
$$iħ\frac{∂Ψ(x,t)}{∂t}=\left(-\frac{ħ^2}{2m}\frac{∂^2}{∂x^2}+V(x)\right)Ψ(x,t)\qquad(18)$$
なる。この方程式をシュレディンガー方程式と言う。
ハミルトニアン演算子
ハミルトニアン演算子を、
$$\hat{H}=-\frac{ħ^2}{2m}\frac{∂^2}{∂x^2}+V(x)\qquad(19)$$
と定義する。そして、(19)を(18)に代入すると、シュレディンガー方程式は、
$$iħ\frac{∂Ψ(x,t)}{∂t}=\hat{H}Ψ(x,t)\qquad(20)$$
となる。
ハミルトニアン演算子の物理的意味は、ハミルトニアン演算子の右から波動関数を掛けると、固有値として波動関数からエネルギーの情報を取り出せることである。
まとめ
波動関数を定義して、シュレディンガー方程式を導出した。また、エネルギー固有値を出すハミルトニアン演算子を導入した。
今回はここまでとして、次回は確率解釈について話したいと思います。
それではまた!!
#量子力学 #波動関数 #シュレディンガー方程式 #ハミルトニアン #たくぶつり
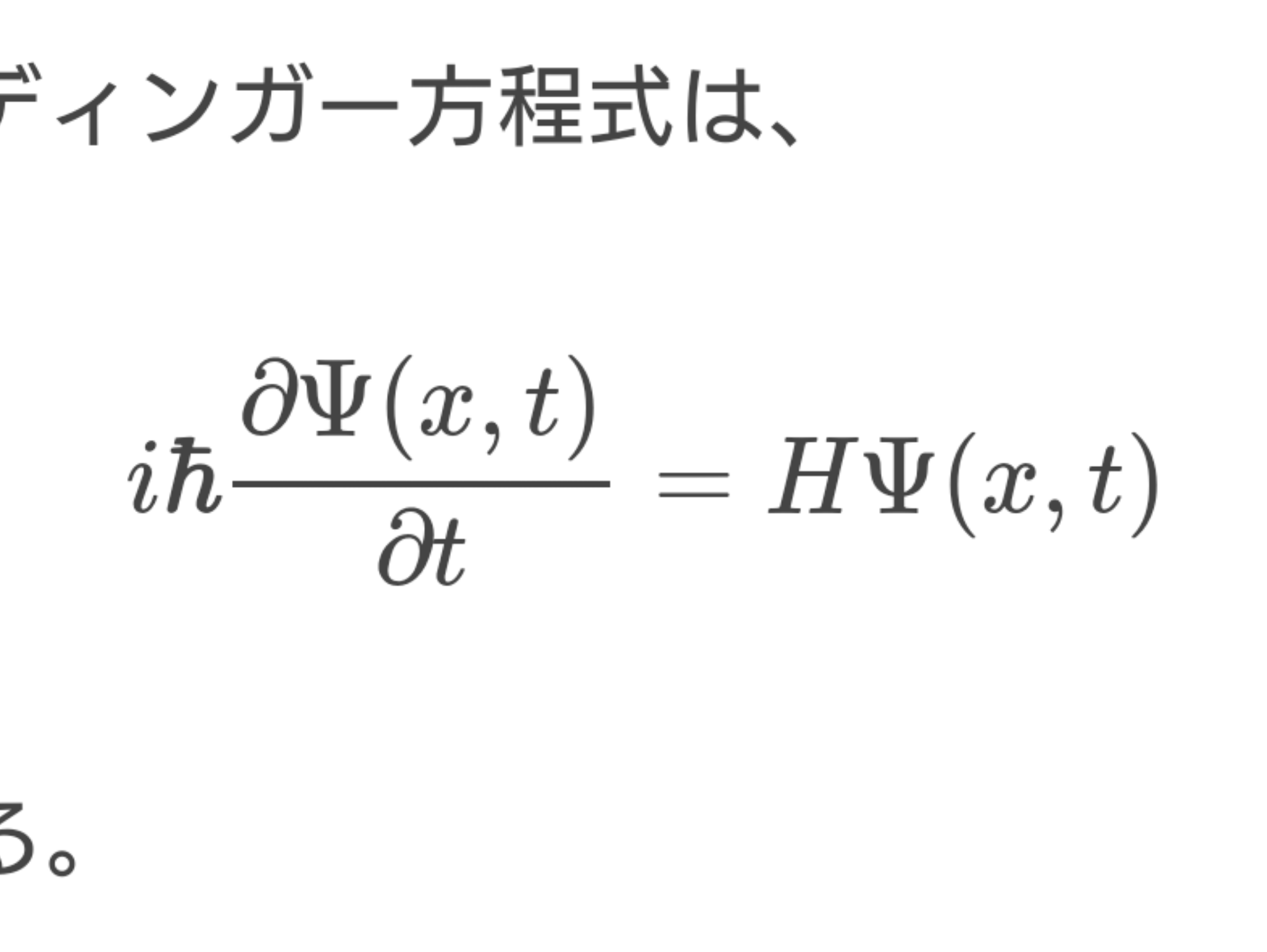

コメント